|
|
|
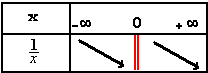
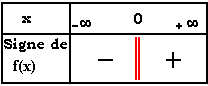
Dans un repère orthonormé, représentons la fonction Clique sur le graphique, puis appuie sur la touche "T" de ton clavier, puis fais varier lentement le nombre p sur l'axe des abscisses. Tous les points tracés ont pour coordonnées ( x , Le point P d'abscisse p décrit la courbe d'équation Cette courbe est appelée hyperbole. Elle admet l'origine comme centre de symétrie. L'axe des abscisses et l'axe des ordonnées sont asymptotes à la courbe. |
|