 |
dossier en cours d'écriture par la 2TH3. Attention risque d'erreurs ! |
|
|
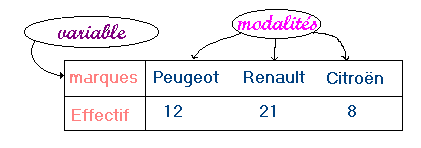
C’est l’étude de la répartition d’un ensemble (de personnes, d’objets, etc … ) appelé population , en fonction d’un caractère ( appelé parfois critère : taille, poids, prix, etc ..).
Les éléments composant la population sont appelés individus.
Etendue
C’est la différence entre les valeurs extrêmes ou bien l’écart entre les 2 valeurs extrêmes de la variable.E = X max – X min
Des indicateurs de position :Moyenne :
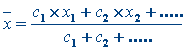
Le Mode ou (classe modale):
C’est la valeur la plus fréquente, c’est à dire ayant le plus grand effectif.
Il a son intérêt si son effectif est nettement supérieur aux autres.
Si deux modalités (ou plus) ont le même plus grand effectif, on dit que la série est bimodale (ou plurimodale)
La médiane :
Elle partage la population en deux groupes de même effectif :
il y a autant d’individus ayant une modalité inférieure à la médiane que d’individus ayant une modalité supérieure à la médiane.
La Fréquence :
C’est le rapport entre l’effectif de la modalité concernée et l’effectif total de la population.
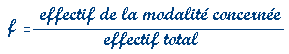
Une fréquence est un nombre compris entre 0 et 1.
La somme de toutes les fréquences est 1.
La fréquence cumulée croissante s’obtient en ajoutant au fur et à mesure les fréquences des modalités précédentes.